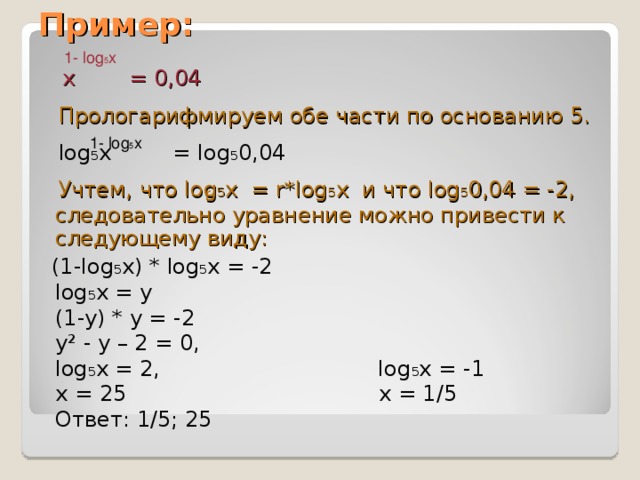
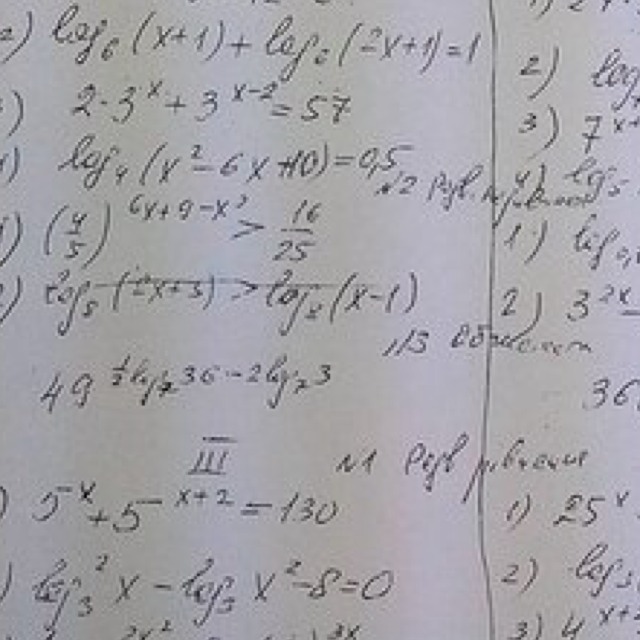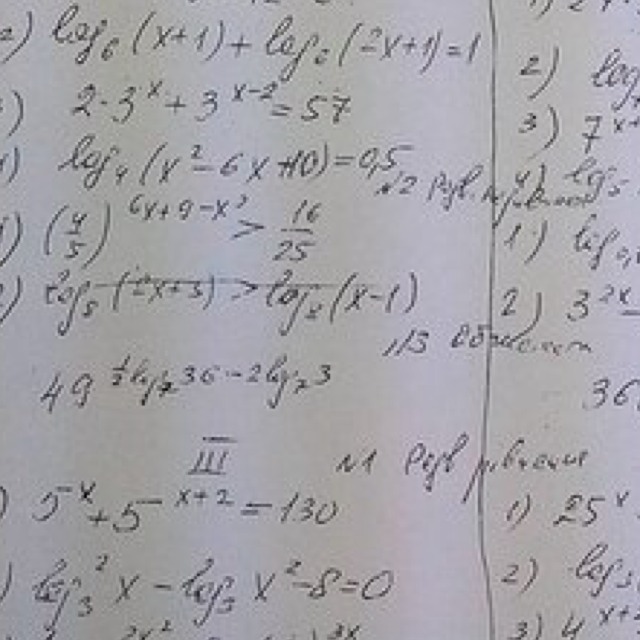5 (x-7) > -1. Log1/6(0,5+x)=-1. Log0. Log6(x+2)<1. Решите уравнение 6log28x 5log8x+1.
|
Log7x. Log 0. 5. Log 0,5 (х+5). 5.
|
5 x -2 0. Log2 2. Log (x+1)/ log2(3x+5)< 1. Log5 (x2+2x -6) = log5 x. Log x x 6 0.
|
5^2x+log2 x=-2. Log_0,2(x^2+3x+1)=0. Log2 1. Log x x 6 0. 2log2/6(x)+5log6(x)+2=0.
|
Log x x 6 0. Log x x 6 0. 5. Лог 5 по основанию х. 5.
|
Log3 1/3. Log x x 6 0. Log0,5(2x+1)-2. Log x x 6 0. Log0 8 3 log3 1.
|
Log 1. Log2 3(x -6) - log2 3 = log3. Log x = 0. 5. Log x x 6 0.
|
Log6(x^2+5x-10)=log6(x+2). Log 6 (x). Log 0. Лог1/3 x > 4. Log 1.
|
Log0 5 x 5 log 2 0 2. Log2 2x log0. Log^2 0,2 x + log0,2 x - 6=0. Log6 (2x2-x)= 1-log6 2. 5.
|
Log x x 6 0. 5. Log 0. Log2 (log6 x) = 1. Log 0.
|
Log^2 5 x-6+x=5log. 5. Лог равен 1. 2 125 решение. Log 0,5 (х+5).
|
125x. Log^2 5 x-6+x=5log. Log x x 6 0. 5. Log 0,2 125.
|
Log x x 6 0. 5 x log 0. Лог1/3 x > 4. Log2 0. Log x x 6 0.
|
Log 0. 5. Log0. Лог2(х+1) -3. 5.
|
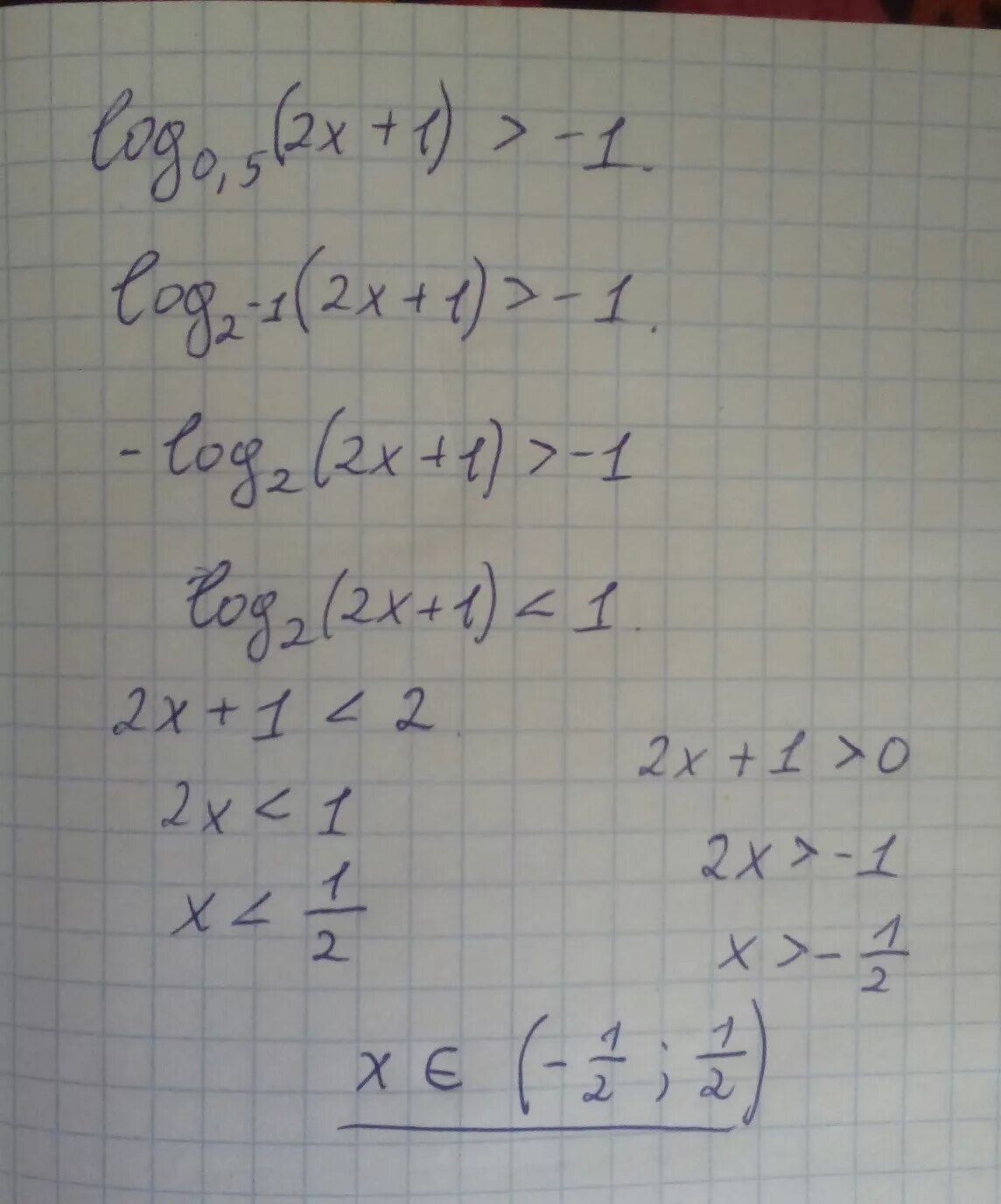Log5x>1. Logx по основанию 5. Log x x 6 0. Log x x 6 0. Log 0,5 2 x − log0,5 x = 6;.
|
5. 0 7 x 2 2 49. 1. Log5 0,125. Логарифм x по основанию 0,5.
|
Log 0,3(5-4x) < log 0,3(x-1) решение. Log1/5(0,5х+3) = - 1. (х+1)log3 6+log3(2 x-1/6)<x-1. Log3. 25.
|
Log 2-x x+2 log x+3 3-x 0. 5. 5. 5. 5.
|
5. Log x x 1 2. Log x x 6 0. 5. Log 2(5x-6) < log 2 2 + 3.
|
Лог x - 6 4 =2. 5. Log 1/2 x. Log5 2 (𝑥 − 1) − log5 2 (𝑥 − 5) ≤ 0. Log05 x2+x -1.
|
